This will be the most scientific and precise post regarding Winston Churchill's belly you'll read today. Maybe all week.
Today, we'll be analyzing the following video:
After randomly embedding the preceding video while thinking about Hooke's Law and the spring constant in my last post, what I, and I'm sure you as well, immediately wonder is, of course, "I wonder what type of spring constant Winston Churchill's belly had?" This seems like something worthy of my time.
Here we go!
If we're going to figure this out, we need some data. First, we need some sense of scale. Since I have no idea the how tall the Animaniacs are, let's focus on the historical figures. I'm going to go with Winston Churchill's height to give the video some scale since he's pretty stretched out whilst his belly is being jumped upon1. It's surprisingly hard to find Churchill's height online with any sort of citation. I found what seems like a pretty solid source (via Wikipedia) for the height of Harry S. Truman (1.75 m). Using that information along with the following picture, I can figure out Churchill's height after throwing the image into Tracker:

Churchill and Truman were nearly the same height. I got 1.76 m (5 ft, 9 in) for Churchill. That seems pretty close to most of the unsourced figures for his height I found online.
I think the best way to go about finding the spring constant for Winston Churchill's belly is to use gravitational potential energy and elastic potential energy. If we can find the gravitational potential energy Stalin has at the top of his bounce and the maximum compression of Churchill's belly, we should be able to do the following:
Where m is Stalin's mass, Δy is Stalin's maximum height above Churchill's belly, and x is the maximum compression of Churchill's belly.
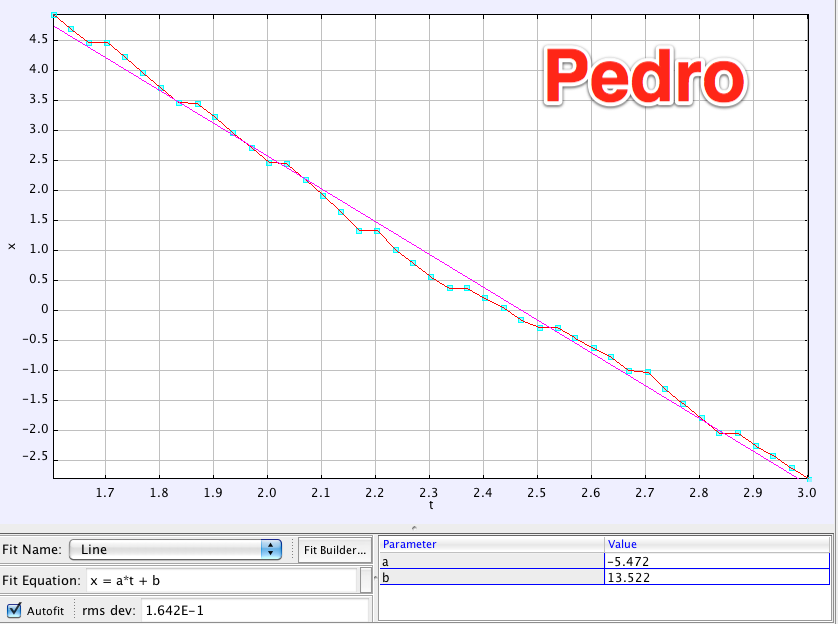
I can fairly easily find Δy and x using Tracker to analyze the video.
![]()
I used 1.70 m for Churchill's height in the video instead of the 1.76 m figure above since his knees are bent slightly. Using that information to scale the video, Stalin's maximum height (Δy) is 0.65 meters and the maximum compression of Churchill's belly (x) is 0.28 m.
Finding Stalin's mass will require another long and probably fruitless internet search. Instead, I'm going to assume from the above picture Stalin is approximately the same height as Harry S. Truman and then assume Stalin's BMI is slightly above average (he was a dictator- which means he has access to lots of food). I'm going to say Stalin's BMI is 26. According to this BMI calculator, that would give Stalin a weight of 175 lbs, or 79.4 kg.
Now we've precisely (ha.) figured out all our variables, so we can go ahead and solve the equation for the spring constant (k):
OK, so what's that mean? It means that if you could compress Winston Churchill's belly by a full meter it would require 12,900 Newtons of force. On the surface of the Earth, that would take a mass of 1,315 kg (2,900 lbs) sitting on his belly to compress it by a full meter2. WolframAlpha helpfully notes that this is approximately a mass equivalent to approximately 2 "typical dairy cows."
We can also learn something about the Animaniacs' collective mass now that we know the spring constant. If we rearrange the previous equation to solve for the mass, we get:
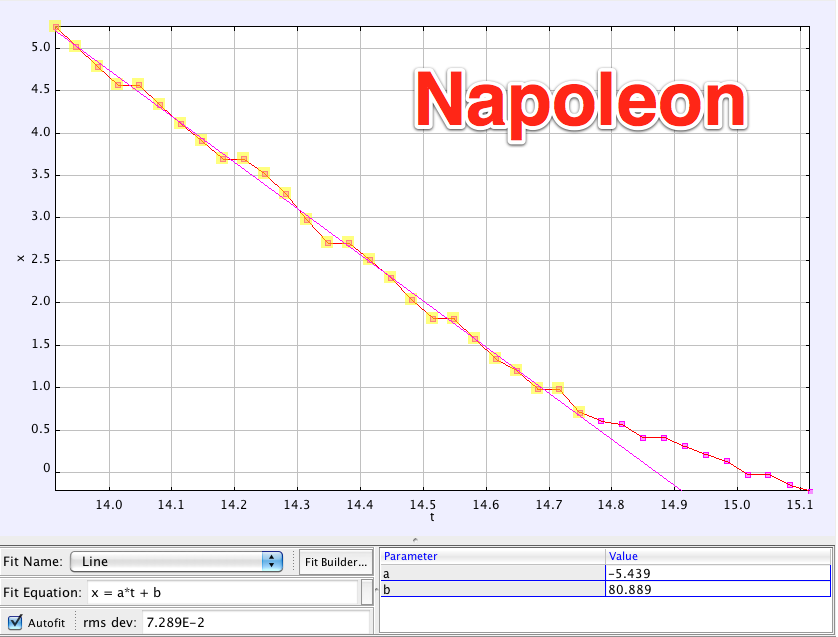
It looks like the maximum height the Animaniacs attain is 0.77 m with a maximum belly compression of 0.16 m. Now solving for the mass we find:
Collectively the three Animaniacs have a mass of 21.9 kg (48.3 lbs). Wow. They're lighter than I anticipated. If you divide that figure evenly by three, the average Animaniac weight is 16.1 lbs. Clearly Dot and Wakko are smaller than Yakko. This may, in fact, prove Dot's hypothesis that in addition to being cute, she's a cat:
Watch animaniacs - what are we? in Animation | View More Free Videos Online at Veoh.com
- Also, I came across a few places that speculated that Stalin may have use elevator shoes to make himself seem taller, so it might be harder to get an accurate figure for him. However, this isn't exactly going to be a super-accuracy fest anyway, so maybe I shouldn't let that bother me. [↩]
- I'm not sure if Churchill actually has a meter of stomach to depress, but you get the idea. [↩]