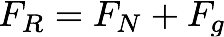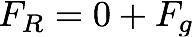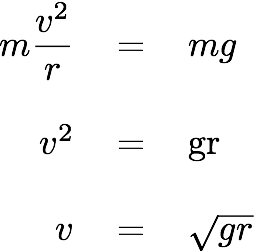I like projects. I really liked this project. The pipe insulation roller coaster project is one of the most enjoyable projects I've ever used in class.
History
It was my second year teaching physics. During the unit on energy, the book we were using frequently used roller coasters in their problems. We even had a little "roller coaster" to use with photo gates. I thought we could do better.
My original idea was to get some flexible Hot Wheels tracks and make some loop-de-loops and hills. Turns out a class set of Hot Wheels track is pretty expensive. On an unrelated yet serendipitous visit to my local big box hardware store, I ran across the perfect (and cheap!) substitute: Pipe Insulation!. For $1.30 or so you can get six feet of pipe insulation- which doubles nicely as a marble track1 when you split the pipe insulation into two equal halves. It's really easy to cut pipe insulation with a sharp pair of scissors. Just be sure you don't buy the "self-sealing" pipe insulation, which has glue pre-applied- it's more expensive and it'd turn into a sticky mess.
At first I planning to simply design a one-period long investigation using the pipe insulation (my original ideas morphed into the pre-activity for this project). As I started to think through the project more and more, I realized we could go way bigger. And thus, the pipe insulation roller coaster project was born.
Building the Coasters
In groups of three, students were given 24 feet of pipe insulation (4 pieces), a roll of duct tape2, and access to a large pile of cardboard boxes3. All groups had to adhere to a few standard requirements:
- Construction requirements
- The entire roller coaster must fit within a 1.0m x 2.0m rectangle4.
- There must be at least two inversions (loops, corkscrews, etc.).
- All 24 feet of pipe insulation must be used.
- The track must end 50 cm above the ground.
- Physics requirements
In addition to meeting the above requirements, students were required to utilize their understanding of the work-energy theorem, circular motion, and friction to do the following: - Determine the average rolling friction, kinetic energy, and potential energy at 8 locations on their roller coaster.
- Determine the minimum velocities required for the marble to stay on the track at the top of all the inversions
- Determine the g-forces the marble experiences through the inversions and at least five additional corners, hills, or valleys.
- The g-forces must be kept at "safe" levels5.

Calculations
- Rolling friction, kinetic energy, and potential energy
- The potential energy ($latex U_g = mgh$) is easy enough to find after measuring the height of the track and finding the mass of the marble. The kinetic energy is trickier and can be done by filming the marble and doing some analysis with Tracker, but since the speed of the marble is likely to be a little too fast for most cameras to pick up clearly, it's probably easier (and much faster) to simply measure the time it takes the marble travel a certain length of track. I describe how this can be done in a previous post, so check that out for more info. That post also includes how to calculated the coefficient of friction by finding how much work was done on the marble due to friction- so I'll keep things shorter here by not re-explaining that process.
- Minimum marble velocities through the inversions.
- Finding g-forces
- Pipe Insulation Roller Coasters and Rolling Friction
- Pipe Insulation Roller Coasters
- Pipe Insulation Roller Coaster Assessment
- The first day we played with pipe insulation in class I had students use some marble-sized steel balls. Unfortunately because the steel balls are so much heavier and the pipe insulation is spongy and flexible, there was just too much friction. When we switched to marbles the next day everything worked like a charm. [↩]
- Most groups typically use more than one roll of duct tape. My first couple years I bought the colored duct tape and gave each group a different color. That was a nice touch, but also a bit more expensive than using the standard silver. Whatever you decide, I highly recommend avoiding the cut-rate duct tape. The cheap stuff just didn't stick as well which caused students to waste a lot of time fixing places where the duct tape fell and in the end used a lot more duct tape. [↩]
- I had an arrangement with our school's kitchen manager to set broken down boxes aside for me for a few weeks before we started the project. If that's not an option, I've also found if you talk to a manager of a local grocery store they're usually more than willing to donate boxes. [↩]
- I made it a requirement for groups to start by building a cardboard rectangle with the maximum dimensions. This served two functions: (1) It made it easy for the groups to see what space they had to work with, and (2) it allows the roller coasters to be moved around a little by sliding them across the floor. [↩]
- Originally I wanted students to keep g-forces below 10. Very quickly it became apparent that under 10g's was overly restrictive and I upped it to 30g's. That's not really safe for living creatures, but it would certainly make it more "exciting." [↩]
- Pro-tip: Have students mark every 10 cm or so on their track before they start putting together their coasters (note the tape marks in this pic). Since d in $latex W=F\cdot d$ in this case is the length of track the marble has rolled so far, it makes finding the value for d much easier than trying to measure a twisting, looping roller coaster track.
- This is also called the critical velocity. That's fitting. If you're riding a roller coaster it's pretty critical that you make it around each loop. Also, you might be in critical condition if you don't. While falling to our death would be exciting, it also limits the ability to ride roller coasters in the future (and I like roller coasters). Since we're primarily concerned with what is happening to the marble at the top of the loop, here's a diagram of the vertical forces on the marble at the very top of the loop:

So just normal force (the track pushing on the marble) and gravitational force (the earth pulling on the marble). Since these forces are both acting towards the center of the loop together they're equal to the radial force:
When the marble is just barely making it around the loop (at the critical velocity), the normal force goes to zero. That is, the track stops pushing on the marble for just an instant at the top of the loop. If the normal force stays zero for any longer than that it means the marble is in free fall, and that's just not safe. So:
Then when you substitute in masses and accelerations for the forces and do some rearranging:
There you go. All you need to know is the radius of the loop, and that's easy enough to measure. Of course, you'd want a little cushion above the critical velocity, especially because we're ignoring the friction that is constantly slowing down the marble as it makes its way down the track.
- An exciting roller coaster will make you weightless and in the next instant squish you into your seat. A really bad roller coaster squishes you until you pass out. This is awesomely known as G-LOC (G-force Induced Loss of Consciousness). With the proper training and gear, fighter pilots can make it to about 9g's before G-LOC. Mere mortals like myself usually experience G-LOC between 4 and 6g's.
As I mentioned, I set the limit for pipe insulation roller coasters at 30g's simply because it allowed more creative and exciting coaster designs. While this would kill most humans, it turns out marbles have a very high tolerance before reaching G-LOC.
To find the g-forces being pulled on corners, loops, or hills you just need to find the radial acceleration (keeping in mind that 1g = 9.8 m/s^2):
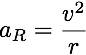
Raise the stakes
Students become fiercely proud of their roller coasters. They'll name them. Brag about them. Drag their friends in during lunch to show them off. Seeing this, I had students show off their creations to any teachers, parents, or administrators that I was able to cajole into stopping by for the official testing of the coasters. I even made up a fun little rubric (.doc file) for any observers to fill out for each coaster. This introduces some level of competition into the project, which gives me pause- though from day one students generally start some friendly smack talk about how their coaster is akin to the Millenium Force while all other coasters are more like the Woodstock Express. The students love to show off their coasters, and it seems the people being shown enjoy the experience as well.

Assessment
Assessment is massively important. However, this post is already long. The exciting conclusion of this post will feature the assessment piece in: Part 2: Pipe Insulation Roller Coaster Assessment.